Microwave and Antenna

This is a summary of Microwave and Antenna course.

绪论

• 微波是电磁波谱中介于超短波和红外线之间的波段，它属于无线电波中波长最短的波段。
• 微波、天线与电波传播是无线电技术的三个重要部分：
  • 微波：引导电磁波在微波传输系统中有效传输，特点是希望电磁波按一定要求沿微波传输系统无辐射地传输。
  • 天线：将导行波变换为空间定向辐射的电磁波；将空间传输的电磁波变为微波设备中的导行波。
  • 电波传播：分析和研究电波在空间的传播方式和特点。

第1章 均匀传输线理论

微波传输线作用是引导电磁波沿一定方向传输，因此又称为导波系统， 其所引导的电磁波被称为导行波。

微波传输线分三类：

• 双导体传输线：传输TEM 波
• 金属波导管：电磁波在管内传播
• 介质传输线：电磁波沿传输线表面传播

1.1 均匀传输线方程及其解

均匀传输线组成的导波系统都可等效为均匀平行双导线系统。

传输线单位长串联阻抗：$Z=R+j\omega L$ <电感是串联的> $Z=R+jX$

传输线单位长并联导纳：$Y=G+j\omega C$ <电容是并联的> $Y=G+jB$

解：

$U(z)=U_+(z)+U_-(z)=A_1e^{jkz}+A_2e^{-jkz}$ 定义 $z=0$ 在负载，正方向向左，向右传播为 $e^{jkz}$ 。

$I(z)=I_+(z)+I_-(z)=\frac{1}{Z_0}({A_1}e^{jkz}-A_2e^{-jkz})​$

传输线上电压和电流以波的形式传播，在任一点的电压或电流均由沿 $-z$ 方向传播的行波（入射波）和沿 $+z$ 方向传播的行波（反射波）叠加而成。

工作参数：

• 特性阻抗$Z_0​$：传输线上导行波的电压电流比。其倒数为特性导纳，用 $Y_0​$ 表示

$$Z_0=\sqrt{\frac{R+j\omega L}{G+j\omega C}} \ \ <L-\mu; C-\varepsilon>$$

​ 对于均匀无耗传输线，$R=G=0​$：

$$Z_0=\sqrt{\frac{L}{C}}$$

​ 常用的同轴线的特性阻抗为 50 $\Omega$ 和 70 $\Omega$

• 传播常数 $\gamma$：导行波传播过程的衰减和相移参数： $$\gamma = \alpha + j \beta$$ 对于无耗传输线，则$\alpha = 0$。$\beta$ 为相移常数，单位为 rad/m <弧度和长度的转化>： $$\gamma=j\beta, \ \beta=\omega\sqrt{LC}$$

• 相速$v_p$：电压、电流入射波（或反射波）等相位面沿传播方向的速度【相速 $m/s$ = 每秒经过的相位 $(rad/s)$ / 相移常数 $(rad/m)$】

  $$v_p=\frac{\omega}{\beta}$$

• 波长$\lambda$：

$$\lambda=\frac{2\pi}{\beta}(=\frac{v_p}{f}=\frac{\lambda_0}{\sqrt{\varepsilon_{r}}}）$$

1.2 传输线阻抗与状态参量

传输线上任意一点的电压与电流值比称为该点的阻抗。

• 输入阻抗：

  $$Z_{in}(z)=Z_0\frac{Z_l+jZ_0tan(\beta z)}{Z_0+jZ_l tan(\beta z)}$$

  $Z_0​$为无耗传输线的特征阻抗，$Z_l​$为终端负载阻抗。

  • 无耗传输线上任意一点的输入阻抗与观察点的位置、特性阻抗、终端负载阻抗与工作频率有关，具有$\lambda /2$重复性。
  • 若 $Z_l​$ 为复数，则传输线上任意点处输入阻抗一般也为复数，但若长度合适，也可变换为实数。传输线的阻抗变换特性。

  

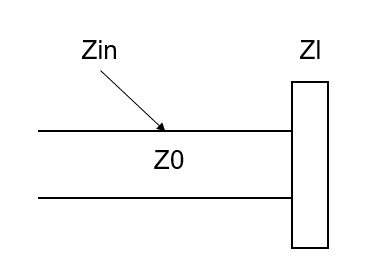
• 反射系数：终端反射系数： $$\Gamma_1=\frac{Z_l-Z_0}{Z_l+Z_0}=|\Gamma_1|e^{j \phi_l}$$ 任意点反射系数可用终端反射系数表示为： $$\Gamma (z)=|\Gamma_1|e^{j(\phi_l-2\beta z)} \ \ <从终端向传输线为z方向，具有重复性>$$ 对均匀无耗传输线来说，任意点反射系数大小相等，只有相位具有$\lambda /2​$重复性。当$Z_l=Z_0​$，负载终端无反射，称为负载匹配。

• 输入阻抗与反射系数的关系：

  $$Z_{in}(z) = Z_0\frac{1+\Gamma(z)}{1-\Gamma(z)} \ \ <Z_{in}(z) \geqslant Z_0 >$$

• 驻波比：终端不匹配时，线上形成驻波。对于无耗传输线，沿线给点的电压和电流振幅不同，以$\lambda /2$周期变化。为描述驻波的大小，引入电压驻波比，定义为波腹点与波节点电压振幅之比。

  $$\rho=\frac{|U|_{max}}{|U|_{min}} = \frac{1+|\Gamma_1|}{1-|\Gamma_1|} \ \ <|\Gamma_1|\geqslant 1>$$

$$|\Gamma_1|=\frac{\rho-1}{\rho+1} \ \ <|\Gamma_1|\leqslant 1>当$|\Gamma_1|=0$，无反射，$\rho=1$；当$|\Gamma_1|=1$，全反射，$\rho=\infty$。$$

​ 当$|\Gamma_1|=0$，无反射，$\rho=1$；当$|\Gamma_1|=1$，全反射，$\rho=\infty$。

1.3 无耗传输线的状态分析

• 行波状态：$|\Gamma_1|=0$，无反射。电压电流振幅不变；电压电流同相；各点阻抗等于特性阻抗。

• 纯驻波状态：$|\Gamma_1|=1​$，分为三种状态

  • 负载短路$Z_1=0$：负载电压min，$z=n\lambda/2​$处为电压波节点
  • 负载开路$Z_1=\infty​$：负载电压max，$z=n\lambda/2​$处为电压波腹点
  • 负载为纯电抗$Z_1=jX_1$：此时终端既不是波腹也不是波节

  沿线各点电压、电流在时间和空间上相差均为 $\pi/2$ ，故它们不能用于微波功率的传输，其输入阻抗为纯电抗特性（代入 $Z_{in}(z)$ 可知）。在 $0<z<\lambda/4$ 内，$Z_{in}=jz$ 相当于一个纯电感；在 $\lambda/4<z<\lambda/2$ 内，$Z_{in}=-jz​$ 相当于一个纯电容；

• 行驻波状态：当微波传输线终端接任意复数阻抗负载时，有信号源入射的电磁波功率一部分被终端负载吸收，另一部分则被反射。

  传输线上任意点输入阻抗表达式为：

  $$Z_{in}(z)=Z_0\frac{Z_1+jZ_0tan(\beta z)}{Z_0+jZ_1tan(\beta z)}$$

  波腹点位置为：

  $$Z_{max}=\frac{\lambda }{4\pi}\phi_l+n\frac{\lambda}{2}，n=0,...$$

  波腹点阻抗为纯电阻：

  $$R_{max}=Z_0\rho$$

  波节点位置为：

  $$Z_{min}=\frac{\lambda }{4\pi}\phi_1 \pm n\frac{\lambda}{2} \pm \frac{\lambda}{4}，n=0,...$$

  波节点阻抗为纯电阻：

  $$R_{min}=\frac{Z_0}{\rho}$$

无耗传输线上距离为$\lambda /4$的任意两点处阻抗的乘积均等于传输线特性阻抗的平方，这种特性称之为$\lambda /4​$阻抗变换性。

$\lambda /2​$重复性：输入阻抗，反射系数

$\lambda /4$阻抗变换性：阻抗乘积等于特性阻抗平方

1.4 传输线的传输功率、效率和损耗

传输功率与效率

传输功率：

$$P_t(z)=P_{in}(z)-P_r(z) \\ P_r(z)=|\Gamma_1|^2e^{-4az}P_{in}(z)$$

设传输总长为 $l​$ ，传输效率：

$$\eta=\frac{负载吸收功率 P_t(0)}{始端传输功率P_t(l)}=\frac{1-|\Gamma_1|^2}{e^{2al}[1-|\Gamma_1|^2e^{-4al}]}$$

传输效率取决于：传输线损耗、终端匹配情况 。当负载与传输线匹配时，传输效率最高。

回波损耗与插入损耗

传输线的损耗可分为：回波损耗和插入损耗

• <增大> 回波损耗：入射波功率与反射波功率之比

  $$L_r(z)=10\lg \frac{P_{in}}{P_r}\ dB=（无耗） -20\lg |\Gamma_1|\ dB \ \ <\frac{U_r}{U_{in}}=\Gamma_1>$$

• <减小> 插入损耗：入射波功率与传输功率之比

  $$L_{i}=10\ lg \frac{P_{in}}{P_t}\ dB = （无耗）10\lg \frac{1}{1-|\Gamma_1|^2} \ \ <P_t=P_{in}-P_{r}>$$

1.5 阻抗匹配

传输线上的三种匹配状态

• 负载阻抗匹配：负载阻抗等于传输线的特性阻抗
• 源阻抗匹配：电源的内阻等于传输线的特性阻抗
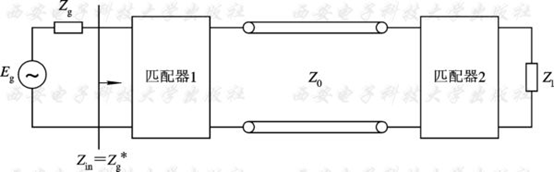
• 共轭阻抗匹配：信源内阻为 $Z_g = R_g+jX_g$，当 $Z_{in}=Z_g^*​$ 时负载得到最大功率值

阻抗匹配的方法

一方面应用阻抗匹配器使信源输出端达到共轭匹配，另一方面应用阻抗匹配器使负载与传输线特性阻抗相匹配。信源端一般采用隔离器，因此重点讨论负载匹配的方法。

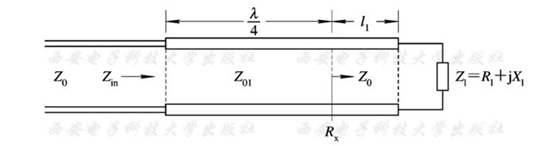
• $\mathbf{\lambda / 4}$ 阻抗变换器法：

  • 当负载阻抗为纯电阻$R_1​$且其值与传输线特性阻抗$Z_0​$不相等时，可在两者之间加接一节长为$\lambda / 4​$、特性阻抗为$Z_{01}​$的传输线实现匹配。由无耗传输线输入阻抗公式可得：$Z_{01}=\sqrt{Z_0R_1}​$。

    

  • 当负载是复阻抗，则先在负载与变换器之间加一段传输线，使变换器的终端为纯电阻，然后用$\lambda/4$阻抗匹配器实现匹配。

    

---

第2章 规则金属波导

第1章从路的观点出发，分析了均匀传输线的基本参数和工作状态，比较适用于同轴线等双导体系统。

对由均匀填充介质的金属波导管组成的规则金属波导，一般采用场分析法。

总结：----------------------------------

Quantity	TEM	TE / TM
$k$	$\omega\sqrt{\mu\varepsilon}$	$\omega\sqrt{\mu\varepsilon}$
$k_c$	0	$\sqrt{(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2}$
$\beta$	$\sqrt{k^2-k_c^2}=k$	$\sqrt{k^2-k_c^2}$

三者关系：$k^2=\beta^2+k_c^2$	三者关系：$\frac{1}{\lambda^2}=\frac{1}{\lambda_g^2}+\frac{1}{\lambda_c^2}$
波数 $k$ ： $k = \frac{2\pi}{\lambda}$，（自由空间）每单位长度波的数量	自由空间波长（工作波长）：$\lambda = \frac{2\pi}{k}$
截止波数 $k_c$	截止波长：$\lambda_c= \frac{2\pi}{k_c}$
相移常数 $\beta$， （实际空间）每单位长度波的数量	波导波长：$\lambda_g = \frac{2\pi}{\beta}$

相速：$v_p=\frac{\omega}{\beta}​$

群速：$v_g=\frac{d\omega}{d\beta}​$

-------------------------------------------

2.1 导波原理

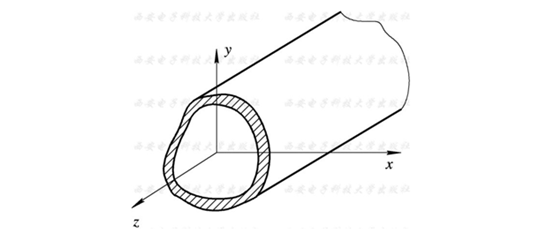
规则金属管内的电磁波

通过电磁场理论，对无源自由空间电场 $E$ 和磁场 $H$ 求解矢量亥姆霍茨方程，通过分离变量法等再结合边界条件，可求得纵向分量 $E_z$ 和 $H_z$ ，进而求出场的横向分量 $E_x$、$E_y$、$H_x$、$H_y$。

有以下结论：

• 满足上述方程和边界条件的解有很多，每一个解对应一个模式，不同的模式具有不同的传输特性

传输特性

• 相移常数 $\beta$ ：

  $$\beta = \sqrt{k^2-k_c^2}，\ \ k=\omega \sqrt{\mu \varepsilon}$$

  截止波数 $k_c​$ ：因为当 $\beta = 0​$， 即导波系统截止时，有 $k_c=k​$ ，因此称 $k_c​$ 为截止波数。该参数是一个与导波系统横截面形状、尺寸及传输模式有关的参量。

  波数 $k​$：$k = \frac{2\pi}{\lambda}​$ 。波数是波长的倒数，另一种描述频率的方式，含义是每单位长度内，波的数量。

• 相速$v_p​$与波导波长$\lambda_g​$

  电磁波在波导中传播，其等相位面移动速率称为相速：

  $$v_p=\frac{\omega}{\beta}$$

  导行波的波长称为波导波长，与波数的关系式为：

  $$\lambda_g = \frac{2\pi}{\beta}$$

• 波阻抗

  定义某个模式的横向电场和横向磁场之比，即：[注：只有横向电磁场对坡印廷矢量有贡献]

  $$Z=\frac{E_t}{H_t}$$

导行波的分类

用以约束或导引电磁波能量沿某一定方向传输的结构称为导波结构，在其中传输的波称为导行波（Guided Wave）。根据截止波数$k_c​$的不同可将导行波分为三种情况：

• $k_c^2=0​$：

  根据$E_x​$、$E_y​$、$H_x​$、$H_y​$的公式可知，此时必有$E_z = 0​$和$H_z=0​$，即只有横向电磁场，称为横电磁波（TEM波）

• $k_c^2>0$：

  这时$E_z$和$H_z$不能同时为0：

  • $E_z\ne 0​$而$H_z=0​$，称为磁场纯横向波（TM波）
  • $E_z = 0​$而$H_z\ne 0​$，称为电场纯横向波（TE波）

2.2 矩形波导

通常将由金属材料制成的、矩形截面的、内充空气的规则金属波导称为矩形波导。

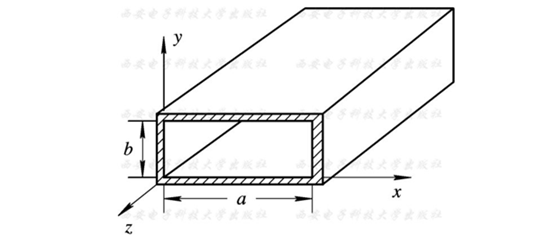
矩形波导中的场

矩形金属波导中只能存在TE波和TM波。

$$k_{cmn}=\sqrt{(\frac{m\pi}{a})^2+(\frac{n\pi}{b})^2}$$

$m​$ 和 $n​$ 分别代表 TE波 沿 $x​$ 方向和 $y​$ 方向分布的半波个数，一组 $mn​$ 对应一种TE波，称为$TE_{mn} \ / \ TM_{mn}​$模

对应截止波长：

$$\lambda_{cTEmn}=\lambda_{cTMmn}=\frac{2\pi}{k_{cmn}}$$

• 当某个模的截止波长 $\lambda_c​$ >工作波长 $\lambda​$ (=$\frac{2\pi}{k}​$) 时，此模可在波导中传输，故称为传导模！

注：如果是TEM波，那么能量是直着传；但如果是TE波，意味着磁场是斜着的，因此能量会在波导内不断反射前行

主模$TE_{10}$的特性

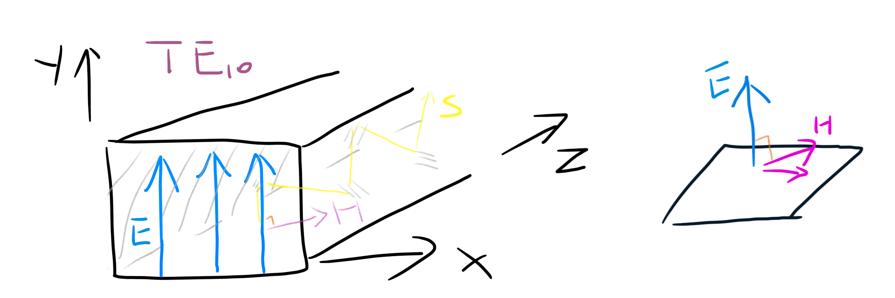
• 截止波数：（代入 $TE​$ 波的 $k_c​$ 定义）

  $$k_c=\frac{\pi}{a}$$

• 截止波长：

  $$\lambda{c}=\frac{2\pi}{k_c}=2a$$

• 相移常数：

  $$\beta=k\sqrt{1-\frac{k_c^2}{k^2}} \Rightarrow \frac{2\pi}{\lambda}\sqrt{1-(\frac{\lambda}{2a})^2}$$

• 波导波长：

  $$\lambda_g=\frac{2\pi}{\beta}=\frac{\lambda}{\sqrt{1-(\frac{\lambda}{2a})^2}}$$

• 波阻抗：

  $$Z_{TE_{10}}=\frac{120 \pi}{\sqrt{1-(\frac{\lambda}{2a})^2}}$$

• 相速：

  $$v_p=\frac{\omega}{\beta}=\frac{v}{\sqrt{1-(\frac{\lambda}{2a})^2}}$$

• 群速：

  $$v_g=\frac{d\omega}{d\beta}=v{\sqrt{1-(\frac{\lambda}{2a})^2}}$$

---

第4章 微波网络基础

在实际微波应用系统中，除了有规则传输系统外，还包含具有独立功能的各种微波元件。

微波网络是在前面分析场分布的基础上，用路的分析方法将微波元件等效为电抗或电阻元件，将实际的导波传输系统等效为传输线，从而将实际的微波系统简化为微波网络。

4.1 等效传输线

在第1章仲，均匀传输理论是建立在 TEM 传输线的基础上的，电压和电流有明确物理意义，且只与纵坐标 $z$ 有关。而实际的非 TEM 传输线如金属波导等，其电磁场 $E$ 与 $H$ 不仅与 $z$ 有关，还与 $x$ 和 $y$ 有关。引入等效电压 和 等效电流 的概念，将均匀传输线理论应用在任意导波系统，这就是 等效传输线 理论。

模式等效传输线

不均匀性的存在使传输系统出现多模传输，但高次模通常不能在传输系统中传输，属于局部场。在离开不均匀处较远的地方设置参考面，从而将不均匀性问题化为等效网络来处理。

4.3 双端口网络的阻抗与转移矩阵

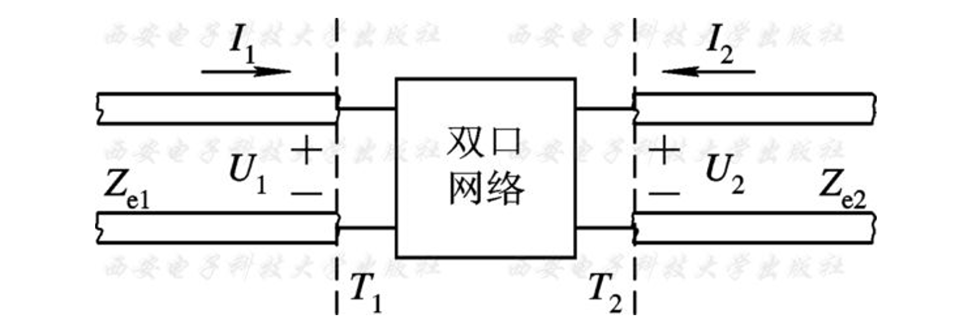
阻抗矩阵$Z$

<电压在左；电流在右；系数为阻抗>

$$\left[ \begin{matrix} U_1\\ U_2 \end{matrix} \right] = \left[ \begin{matrix} Z_{11} & Z_{12}\\ Z_{21} & Z_{22} \end{matrix} \right] \left[ \begin{matrix} I_1\\ I_2 \end{matrix} \right]$$

对于互易网络有 $Z_{12}=Z_{21}​$

对于对称网路有 $Z_{11}=Z_{22}​$

将个端口的电压和电流分别对 自身特性阻抗 归一化，则有： 【小写表明为归一化】

$$[u]=[\bar{z}][i]\\ u_1=\frac{U_1}{\sqrt{Z_{e1}}}, \ i_1=I_1\sqrt{Z_{e1}} \\ u_2=\frac{U_2}{\sqrt{Z_{e2}}}, \ i_2=I_2\sqrt{Z_{e2}}$$

导纳矩阵$Y$

<电流在左；电压在右；系数为导纳>

$$\left[ \begin{matrix} I_1\\ I_2 \end{matrix} \right] = \left[ \begin{matrix} Y_{11} & Y_{12}\\ Y_{21} & Y_{22} \end{matrix} \right] \left[ \begin{matrix} U_1\\ U_2 \end{matrix} \right]$$

对于互易网络有 $Y_{12}=Y_{21}​$

对于对称网路有 $Y_{11}=Y_{22}​$

归一化：

$$[i]=[\bar{y}][u]\\ i_1=\frac{I_1}{\sqrt{Y_{e1}}}, \ u_1=U_1\sqrt{Y_{e1}} \\ i_2=\frac{I_2}{\sqrt{Y_{e2}}}, \ u_2=U_2\sqrt{Y_{e2}}$$

转移矩阵$ABCD$

<左侧在左；右侧在右；系数为如何转移>

$$\left[ \begin{matrix} U_1\\ I_1 \end{matrix} \right] = \left[ \begin{matrix} A & B\\ C & D \end{matrix} \right] \left[ \begin{matrix} U_2\\ -I_2 \end{matrix} \right]$$

归一化：

$$\left[ \begin{matrix} u_1\\ i_1 \end{matrix} \right] = \left[ \begin{matrix} a & b\\ c & d \end{matrix} \right] \left[ \begin{matrix} u_2\\ -i_2 \end{matrix} \right]$$

对于互易网络有 $AD-BC=ad-bc=1$

对于对称网路有 $a=d$

n个双端口网络级联，有 $[A] = [A_1][A_2]…[A_n]​$

输入阻抗： （转移矩阵特有）

$$Z_{in}=\frac{AZ_l+B}{CZ_l+D}$$

$Z_l​$为输出端负载。

4.4 散射矩阵与传输矩阵

前面三种网络矩阵建立在$U, I​$基础之上，微波频率下失去明确的物理意义，另外要求端口开路/短路难以实现。由于可以测量入射波和反射波的相对大小和相对相位，散射矩阵和传输矩阵就是基于入射波/反射波 基础的。

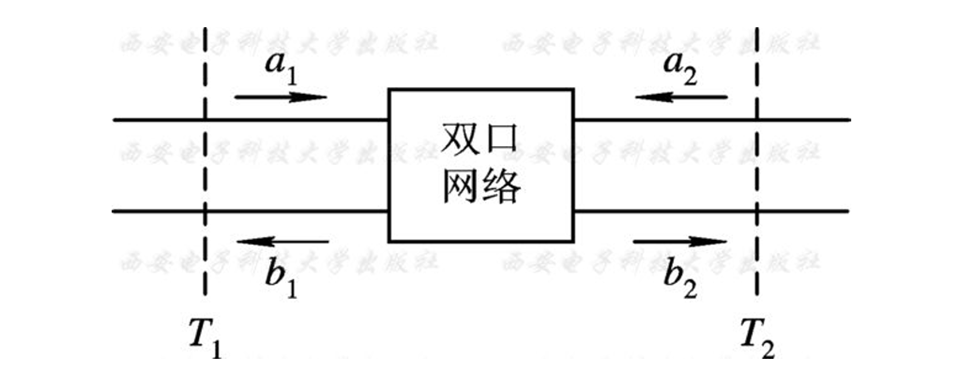
定义 $a_i$ 为入射波电压的归一化值，其有效值的平方等于入射波功率；定义 $b_i$ 为反射波电压的归一化值，其有效值的平方等于反射波功率。这样端口1的归一化电压可表示为 $u_1=a_1+b_1$，归一化电流可表示 $i_1=a_1-b_1​$。【小写表明为归一化】

散射矩阵$S$

<入射在右；反射在左；系数为各种散射>

$$\left[ \begin{matrix} b_1\\ b_2 \end{matrix} \right] = \left[ \begin{matrix} S_{11} & S_{12}\\ S_{21} & S_{22} \end{matrix} \right] \left[ \begin{matrix} a_1\\ a_2 \end{matrix} \right]$$

参数建立在端口接匹配负载基础上的反射系数或传输系数。$S_{11}$ 表示端口2匹配时，端口1的反射系数，$S_{22}$ 为端口2的反射系数，$S_{12}$ 为端口2到端口1的反向传输系数，$S_{21}$ 为端口1到端口2的正向传输系数。

互易网络：$S_{12}=S_{21}​$

对称网络：$S_{11}=S_{22}​$

无耗网络：$[S]^{共轭转置}[S]=[E]$ (散射矩阵特有)

回波损耗：$L_r=20\lg |\frac{a_1}{b_1}|=-20\lg |S_{11}|​$

插入损耗：$L_i=20\lg |\frac{a_1}{b_2}|=20\lg |S_{21}|​$

传输矩阵$T$

<左侧在左；右侧在右；系数为如何转移>

$$\left[ \begin{matrix} a_1\\ b_1 \end{matrix} \right] = \left[ \begin{matrix} T_{11} & T_{12}\\ T_{21} & T_{22} \end{matrix} \right] \left[ \begin{matrix} b_2\\ a_2 \end{matrix} \right]$$

传输矩阵用于网络级联时比较方便。

散射参量与其他参量之间的相互转换

由于 $[S]$ 定义在归一化入射波电压和电流的基础上，因此与其他参量的归一化值之间转换比较容易

已知条件：

• $u_1=a_1+b_1$, $i_1=a_1-b_1$
• 两个矩阵的展开表达式

$[S]$ 与 $[\bar{z}][\bar{y}]$ 的转换, $[S]$ 与 $[a]​$ 的转换：

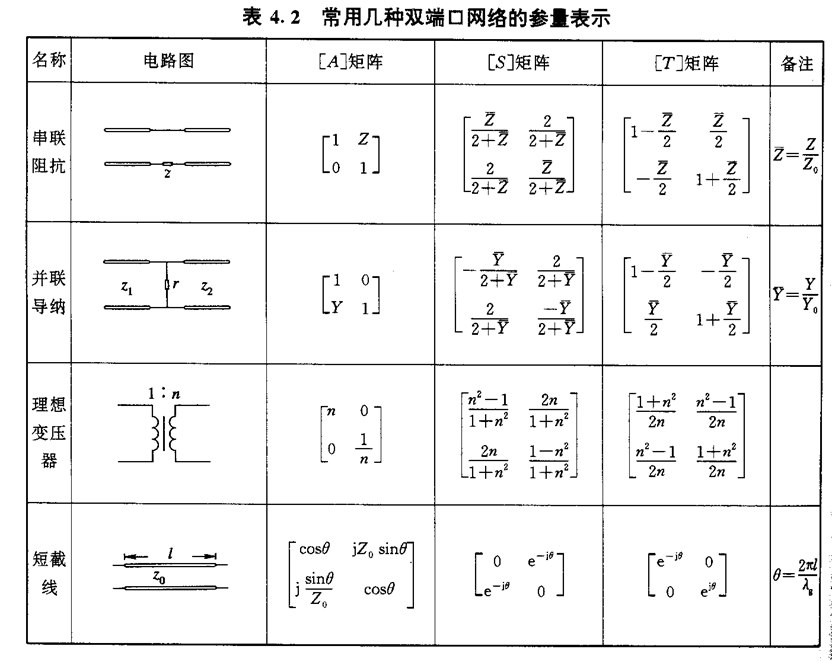
短截线 $[A]$： <开路>

$U(z)=e^{j\beta z}+e^{-j\beta z}​$

$I(z)=\frac{e^{j\beta z}}{Z_0}-\frac{e^{-j\beta z}}{Z_0}$

<短路>

$U(z)=e^{j\beta z}-e^{-j\beta z}​$

$I(z)=\frac{e^{j\beta z}}{Z_0}+\frac{e^{-j\beta z}}{Z_0}$

---

第5章 微波元器件

5.1 连接匹配元件

三大类：

1. 终端负载元件：连接在传输系统终端实现终端短路、匹配或标准失配等功能
2. 微波连接原件：将两个微波系统按一定的要求连接起来
3. 阻抗匹配元器件：调整传输系统与终端之间阻抗匹配

终端匹配元件

• 短路负载：对金属波导最方便的短路负载是终端接一块金属片，但实际往往需要调节短路面位置。
• 匹配负载：几乎能全部吸收输入功率的单端口元件，e.g. 楔形吸收体。
• 失配负载：吸收一部分又反射一部分微波功率。

微波连接元件

• 波导接头：接触不良时，接触电阻大，纵向电流经过连接处时会产生很大大功率损耗（扼流法兰接头利用 $\lambda / 4​$ 阻抗变换解决）；电磁波在接触不良时反射很大。

• 理想衰减器：

  <互易> 本来是 $e^{- \gamma l}=e^{-(\alpha+j \beta)l}​$ ，因 $\alpha \gg \beta​$

  $$[S_\alpha]= \left[ \begin{matrix} 0 & e^{-\alpha l}\\ e^{-\alpha l} & 0 \end{matrix} \right]$$

• 理想相移元件：本来是 $e^{-\gamma l}=e^{-(\alpha+j \beta)l}$ ，因 $\alpha =0$ ，$\theta=\beta l = \frac{2\pi}{\lambda_g}l$ $$[S_\theta]= \left[ \begin{matrix} 0 & e^{-j \theta}\\ e^{-j\theta } & 0 \end{matrix} \right]$$

• 理想隔离器： $$[S]= \left[ \begin{matrix} 0 & 0\\ 1 & 0 \end{matrix} \right]$$

阻抗匹配元件

• 螺钉调配器：螺钉是低功率微波装置中普遍采用的调谐和匹配元件，它是在波导宽边中央插入可调螺钉作为调配元件。多个相距一定距离的螺钉可构成螺钉阻抗调配器。（支节调配原理）
• 多阶梯阻抗变换器：组成多个 $\lambda / 4​$ 阻抗匹配器，从而扩宽频带。

5.2 功率分配与合成器件

两大类：

1. 功率分配元件【定向耦合器、功率分配器、波导分支器】：将一路微波功率在一定频段内按比例分成几路
2. 多工器/合路器：将几个不同窄频段的信号合成一路宽频信号

这些元件一般为线性多端口互易网络。

定向耦合器

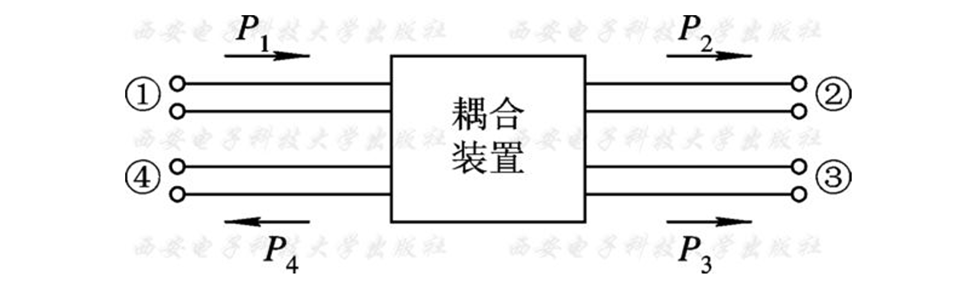
定向耦合器是四端口网络，端口“①”为输入端，端口“②”为直通输出端，端口“③”为耦合输出端，端口“④”为隔离端。“①、②”是主线；“③、④”是副线。

p.s.: 耦合指从主线上取能量，例如从天线发射的主线上取少部分能量进行监测。

• 耦合度：

  $$C=10\lg\frac{P_1}{P_3}=20\lg\frac{1}{|S_{13}|}\ dB$$

• 隔离度：

  $$I=10\lg\frac{P_1}{P_4}=20\lg\frac{1}{|S_{14}|}\ dB$$

• 定向度：

  $$D=10\lg\frac{P_3}{P_4}=20\lg|\frac{S_{13}}{S_{14}}|\ dB$$

• 输入驻波比：

  端口“②、③、④”都接匹配负载时的输入端口“①”的驻波比

  $$\rho=\frac{1+|S_{11}|}{1-|S_{11}|}$$

例：波导双孔定向耦合器

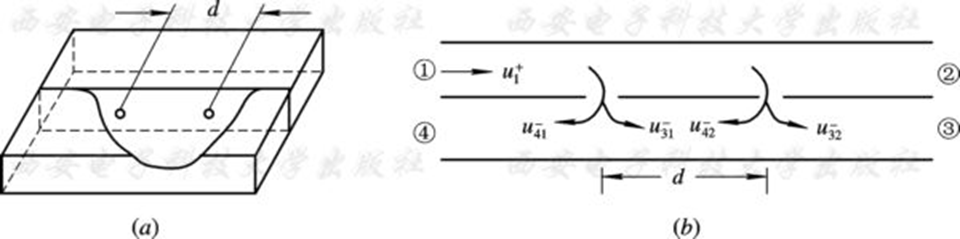
两小孔相距 $\lambda / 4$ ，耦合端 $u_{31}^-， u_{32}^-$ 同向叠加，隔离端 $u_{41}^-， u_{42}^-$ 反向抵消。

功率分配器

例：微带环形电桥

$$[S]=\frac{1}{\sqrt{2}} \left[ \begin{matrix} 0 & -j & 0 &-j\\ -j & 0 & j &0\\ 0 & j & 0 &-j\\ -j & 0 &-j & 0 \end{matrix} \right]$$

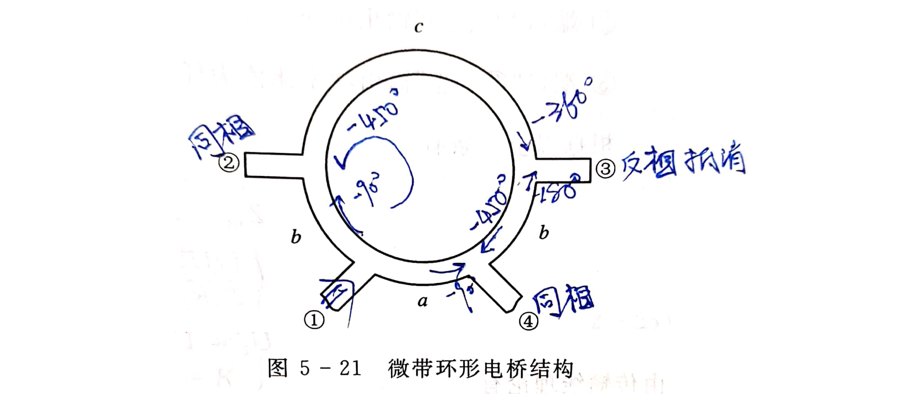
例如 $S_{41}=\frac{b_4}{a_1}= -j​$ 即从①输入在④端口有输出且相位滞后$-90^\circ​$：两个方向一个为 $-90^\circ​$ ， 一个为 $-450^\circ​$ ，同向叠加且滞后 $-90^\circ​$ 。

波导分支器

例：E - T 分支

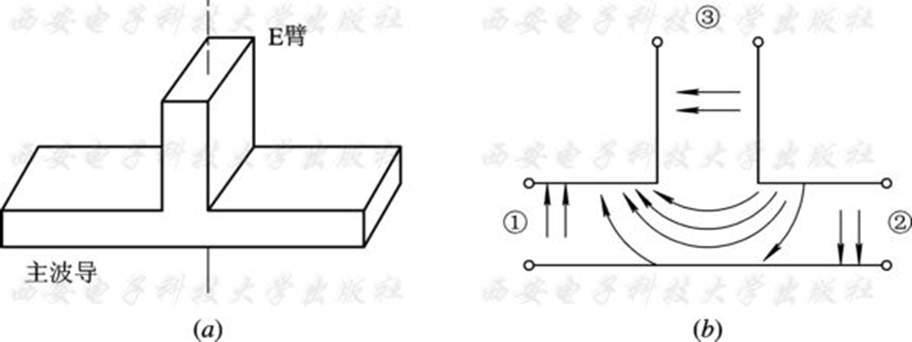
其轴线平行于主波导的 $TE_{10}​$ 模的电场方向。当微波信号从端口“③”输入时, 平均地分给端口“①、②”, 但两端口是等幅反相的; 当信号从端口“①、②”反相激励时, 则在端口“③”合成输出最大; 而当同相激励端口“①、②”时, 端口“③”将无输出。

例：H - T 分支

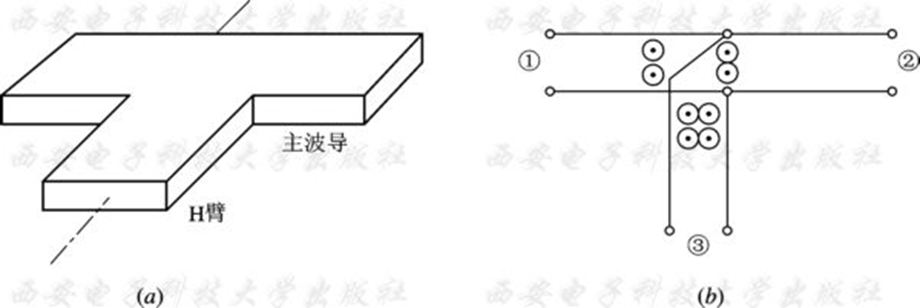
其轴线平行于主波导的 $TE_{10}$ 模的磁场方向。当微波信号从端口“③”输入时, 平均地分给端口“①、②”, 这两端口得到的是等幅同相的 $TE_{10}​$ 波; 当在端口“①、②”同相激励时, 端口“③”合成输出最大, 而当反相激励时端口“③”将无输出。

5.3 微波谐振器件

腔体的长度 $l$ 和波导波长 $\lambda_g​$ 应满足

$$l=p\frac{\lambda_g}{2}\ \ \ p=(1,2,...)$$

矩形空腔谐振器

• 谐振频率：对 $TE_{101}$ 模，$\lambda_c=2a$ （最大波长为p=1时），谐振频率

$$f_0=\frac{c\sqrt{a^2+l^2}}{2al}$$

---

第6章 天线辐射与接收的基本理论

6.1 概论

用来辐射和接收无线电波的装置称为天线，发射机产生的已调制的高频电流能量（或导波能量）经馈线传输到发射天线，通过天线将其转换为某种极化的电磁波能量。

天线的四个最基本功能：

1. 尽可能多将导波能量转为电磁波能量
2. 具有方向性
3. 有适当的极化
4. 有足够的工作频带

6.2 电基本振子的辐射

电基本振子是一段长度 $l​$ 远小于波长、电流 $I​$ 振幅均匀分布、相位相同的直线电流元。它是线天线的基本组成部分。

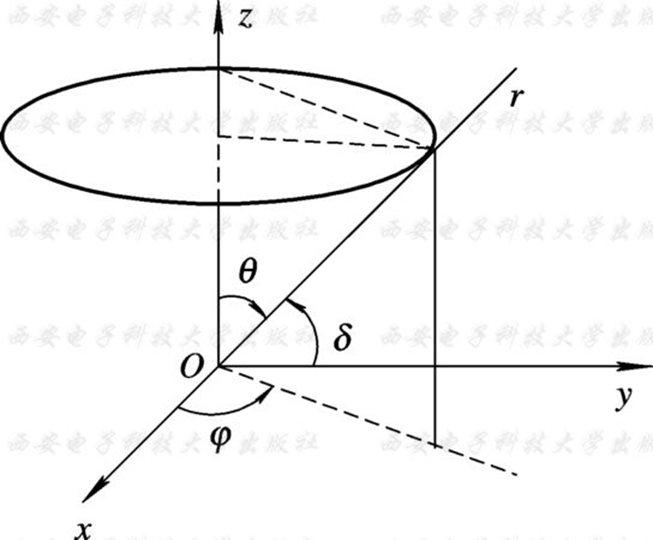
分析远区场（辐射场），是沿着径向向外传播的横电磁波。对坡印廷矢量有贡献的是 $E_\theta$ ：

$$E_\theta=j\frac{k^2Il}{4\pi \omega\varepsilon_0r}（E_0） \ sin\theta (方向性) \ e^{-jkr} （相位滞后）$$

6.3 天线的电参数

天线的电参数就是能定量表征其能量转换和定向辐射能力的量。

天线方向图及其有关参数

天线方向图是指离天线一定距离处，辐射场的相对场强（归一化模值）随方向变化的曲线图。

1. $E$ 平面，即电场矢量所在平面。对于沿 $z$ 轴放置的电基本振子而言，子午平面就是 $E​$ 平面。
2. $H​$ 平面，即磁场矢量所在平面。对于沿 $z​$ 轴放置的电基本振子而言，赤道平面就是 $H​$ 平面。

e.g. 沿 $z​$ 轴放置的电基本振子的 $E​$ 平面和 $H​$ 平面：

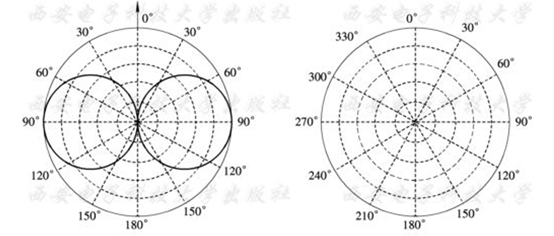
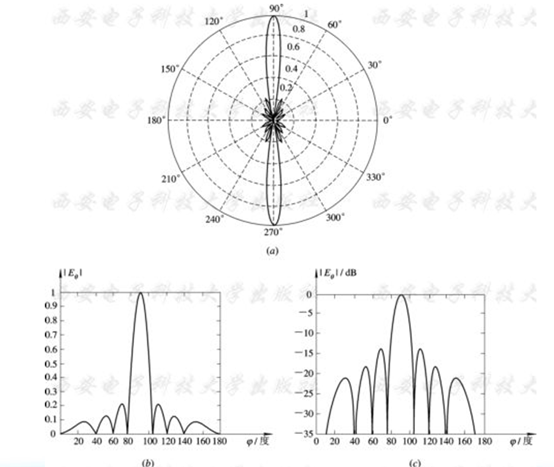
• 主瓣宽度：衡量天线的最大辐射区域的尖锐程度的物理量。在场强方向图中，等于最大场强的 $1/\sqrt{2}$ 两点之间的宽度，称为半功率波瓣宽度。

• 旁瓣电平：离主瓣最近且电平最高的第一旁瓣电平，一般以分贝表示。旁瓣电平尽可能低。

• 前后比：最大辐射方向电平与其相反方向电平之比，一般以分贝表示。

• 方向系数 $D$：在离天线某一距离处，天线在最大辐射方向上的辐射功率流密度 $S_{max}$ 与相同辐射功率的无方向性天线在同一距离处的辐射功率功率流密度 $S_0$ 之比。

$$D=\frac{S_{max}}{S_0}=\frac{|E_{max}|^2}{|E_0|^2}$$

天线效率

天线效率定义为天线辐射功率与输入功率之比，记为 $\eta_{A}​$ ，即

$$\eta_A=\frac{P_{\Sigma}}{P_i}=\frac{P_\Sigma}{P_\Sigma+P_l}$$

$P_i$ 为输入功率，$P_\Sigma$ 为辐射功率，$P_l​$ 为欧姆损耗。

辐射功率与辐射电阻的关系为：

$$P_\Sigma=\frac{1}{2}I_m^2 R_\Sigma$$

天线效率与辐射电阻 $R_\Sigma​$ 和 $R_l​$ 的关系：

$$\eta_A=\frac{R_{\Sigma}}{R_{\Sigma}+R_l}$$

增益系数

增益系数是综合衡量天线能量转换和方向特性的参数，记为 $G$ ：

$$G=D \cdot \eta_A$$

6.4 接收天线理论

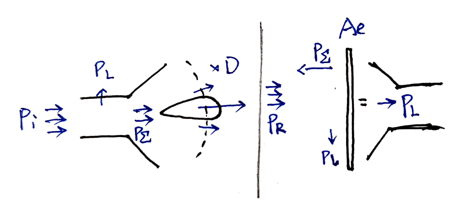
天线接收功率

$$P_R=P_\Sigma+P_L+P_l$$

其中， $P_\Sigma$ 为接收天线的再辐射功率； $P_L$ 为负载吸收的功率； $P_l$ 为导线和媒质的损耗功率。

有效接收面积

有效接收面积是衡量一个天线接收无线电波能力的重要指标。它的定义为：当天线以最大接收方向对准来波方向进行接收时，接收天线的总接收功率 $P_R$ （参考Microwave Engineering） (课本：接收天线传送到匹配负载的平均功率为 $P_{Lmax}$ 即无损) ，并假设此功率是由一块与来波方向相垂直的面积所截获，则这个面积称为接收天线的有效接收面积，记为 $A_e$：

$$A_e=\frac{P_{R}}{S_{av}}$$

其中， $S_{av}​$ 为入射到天线上电磁波的时间平均功率流密度。

$$A_e=\frac{\lambda^2 D}{4\pi} (不考虑天线损耗) \\ A_e=\frac{\lambda^2 G}{4\pi} (考虑天线损耗)$$

有效接受面积与来波波长 $\lambda$ 和接收天线的方向系数 $D$ 有关。

---

第7章 电波传播概论

7.1 电波传播的基本概念

发射天线的输入功率为 $P_i$ ，辐射功率为 $P_\Sigma$ ，若以 $G_i$ 表示实际天线的增益系数；接收天线的增益系数为 $G_R$ ，有效接收面积为 $A_e$ ，则在距离发射天线 $r​$ 处的接收天线所接收的功率为：

$$P_R=S_0 \cdot {A_e} =\frac{P_iG_i}{4 \pi r^2}\cdot \frac{\lambda^2 G_R}{4\pi}$$

将输入功率与接收功率之比定义为自由空间的基本传输损耗，即

$$L_{bf}=\frac{P_i}{P_R}=(\frac{4\pi r}{\lambda})^2 \cdot \frac{1}{G_i G_R}$$

---

第8章 线天线

8.2 阵列天线

二元阵

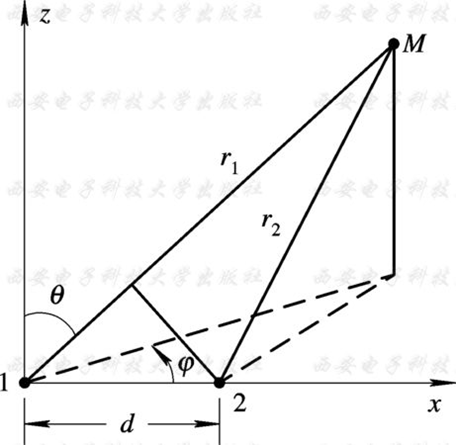
设天线阵是由间距为 d 并沿 x 轴排列的两个相同的天线元所组成。假设天线元由振幅相等的电流所激励, 但天线元2的电流相位超前天线元1的角度为 ζ, 它们的远区电场是沿 θ 方向的, 于是有

$$E_{\theta 1}=E_m F(\theta, \phi) \frac{e^{-jkr_1}}{r_1} \\ E_{\theta 2}=E_m F(\theta, \phi) \frac{e^{-jkr_2}}{r_2}\\ |E_\theta|=\frac{2E_m}{r_1}\ |F(\theta, \phi)|\ |cos\frac{\psi}{2}|，\ \psi=kd \ sin\theta \ cos\varphi \ + \zeta$$

式中，$|F(\theta, \phi)|$ 称为元因子，表示组成天线阵的单个辐射元的方向图函数，其值仅取决于天线元本身的类型和尺寸。

$ |cos\frac{\psi}{2}|​$ 称为阵因子，表示各向同性元所组成的天线阵的方向性, 其值取决于天线阵的排列方式及其天线元上激励电流的相对振幅和相位, 与天线元本身的类型和尺寸无关。

两者相乘为天线阵的方向图函数。

如果天线阵由沿 $x$ 轴排列且平行于 $z$ 轴放置的半波振子组成，只需要将元因子即半波振子的方向函数 $F(\theta)=\frac{cos(\frac{\pi}{2}cos\theta)}{sin\theta}$ 代入，有

$$|E_\theta|=\frac{2E_m}{r_1}\ |\frac{cos(\frac{\pi}{2}cos\theta)}{sin\theta}|\ |cos\frac{\psi}{2}|$$

二元阵的 $E$ 面方向图函数： （令 $\varphi=0$）[两振子所在平面]

$$|F_E(\theta)|=|\frac{cos(\frac{\pi}{2}cos\theta)}{sin\theta}|\ |cos\frac{kd \ sin\theta \ + \zeta}{2}|$$

二元阵的 $H$ 面方向图函数： （令 $\theta=\frac{\pi}{2}$）[两振子垂直平面]

$$|F_H(\varphi)|=|cos\frac{kd \ cos\varphi \ + \zeta}{2}|$$

8.3振子天线

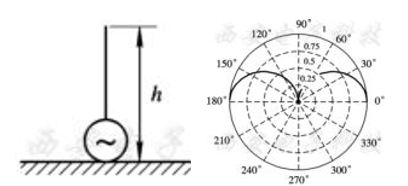
提高单极天线效率的方法：

• 提高天线的辐射电阻：在顶端加容性负载或在底端加感性负载，提高了天线上波辅点的位置，等效增加天线的有效高度。
• 降低损耗电阻

8.4引向天线与电视天线

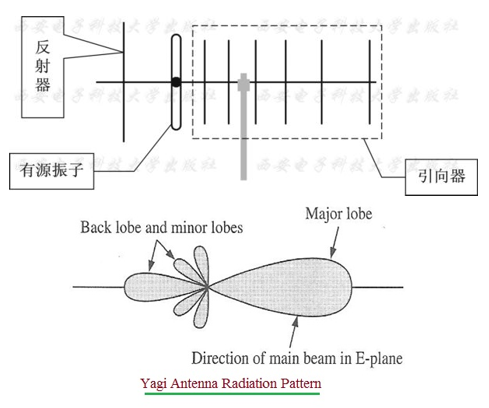
​ 反射器略长于半波长，因此呈感性，其感应电流滞后于感应电动势90°。振子位于反射器前方四分之一波长处，其感应电动势超前反射器的感应电动势90°，而因为振子谐振，所以振子的电动势同电流同相。因此振子电流超前反射器电流180°，而反射器电流所感应出的磁场落后电流90°，感应磁场在振子上感应的电动势比磁场本身落后90°。最终，反射器在振子上的感应电动势同振子自身的感应电动势同相，二者叠加增强。引向器也依据类似的原理加强了振子的感应电动势。

优点：方向性强，增益高。广泛用在米波和分米波段的电视接收天线。

缺点：频带较窄

电视发射天线的特点：

• 频带范围宽
• 采用水平极化，即天线及其辐射电场平行于地面。因工业干扰大多是垂直极化波

8.5 移动通信基站天线

特点：

• 为使用户在移动状态下使用方便，采用垂直极化
• 增益高

8.6 螺旋天线

螺旋天线是常用的圆极化天线。

螺旋天线的辐射特性与螺旋的直径有密切关系。

1. $d/\lambda<0.18$ 法向模式：天线的最大辐射方向在螺线轴线垂直的平面内。辐射效率和增益低，超短波手持式通信机。
2. $d/\lambda \approx 0.25\sim 0.45​$ 轴向模螺旋天线。一圈的周长接近一个波长，此时天线上的电流呈行波分布，则天线的辐射场呈圆极化，最大辐射方向沿轴线方向。
3. $d/\lambda> 0.5$ 圆锥型模式天线。

8.7 行波天线

如果天线上电流分布是行波，则为行波天线。（振子型天线则是驻波）

行波天线由导线末端接匹配负载来消除反射波

优点：单向辐射特性、较高的增益、较宽的带宽、超短波波段

缺点：能量被负载吸收，天线效率不高

8.8 宽频带天线

平面等角螺旋天线：

• 保持宽频带
• 原极化特性

8.10 微带天线

优点：一致性好，易于集成

缺点：方向系数低，频带窄，损耗大，交叉极化大