Welcome to my note on CS231n! In this note, I summarize the key points in this course with my comments. Supplemental tutorials by other experts are also provided to grasp a deeper understanding of this field. Let’s find out how to empower machine vision with deep learning!
L2: Image Classification
K-Nearest Neighbor
不太好在于只是把注意力放在distance; 而且为了密集填充区域,随着维度上升,需要的数据点就会指数增加
Linear classification
parameter好处在于测试时不用考虑数据集,只用考虑x,W
bias 在数据不平衡时起作用
缺点是只有一个template
Cross Validation


原理实际上是:为了使得训练出来的模型稍微复杂些适应现实情况,又不能太复杂以至于泛化性差,我们需要有一定数据去测试模型的效果。但是我们不能用test的数据,毕竟这有点作弊了,于是我们在训练集中划分出folds(羊群),取其中一个作为假定的test数据集进行检验。然后换着fold作为测试对象。最终将总的误差求平均作为模型误差值!

举个例子:横轴为多项式次数,当次数越高,虽然在训练集上效果越好,但是交叉验证的结果很差,证明次方数高时,其泛化性是很低的。
Others


L3: Loss Functions and Optimization
Loss Functions

计算错误判断的label的值-正确label的值+1,若此值小于0,意味着正确label的区分度好,loss=0;若此值大于0,意味着label区分度差,loss等于此值。


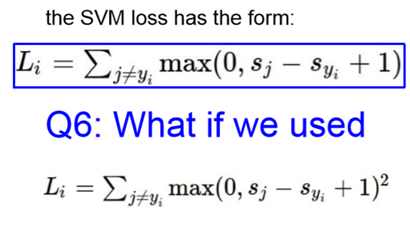
选择loss function的方式在于如何衡量误差
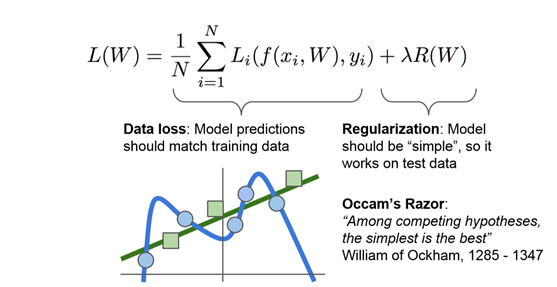
鼓励将模型简单化,引入regularization 其中λ是超参数:超参数是在开始学习过程之前设置值的参数,而不是通过训练得到的参数数据。通常情况下,需要对超参数进行优化,给学习机选择一组最优超参数,以提高学习的性能和效果。

当使用复杂模型时,会被惩罚。

Softmax函数作为loss function是另外一种选择。其值介于0-1,sum=1。

loss function是为了最小化,因此取-log进行优化。
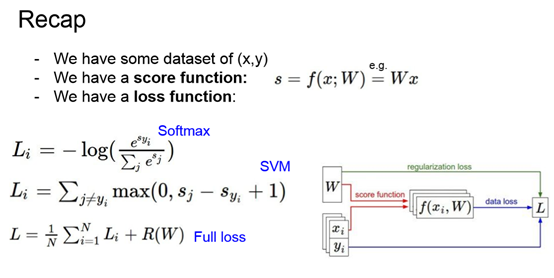
SVM loss 的特点在于,如果正确label已经具有很好区分度(过了bar线之后就放弃了),那么loss=0,即使改变正确label对应的值,也不影响loss。
而Softmax特点是始终希望正确label的值在经过softmax函数后趋向于1,意味着始终希望预测结果全部都落在正确label上。
Optimization


运用batch减少优化时的计算量
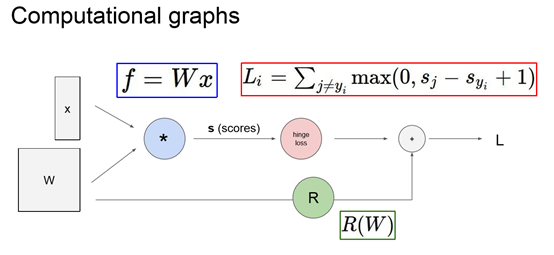
L4: Introduction to Neural Networks
Neuron
注:关于如何理解神经元个数和特征
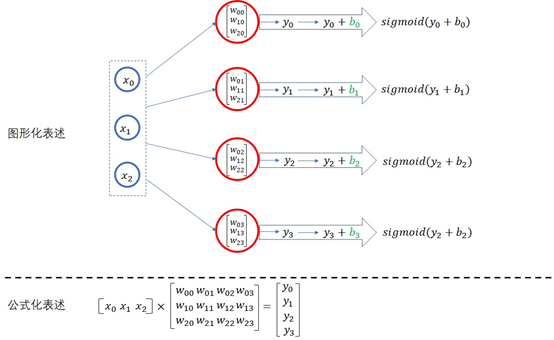
XW矩阵,W的行数与X匹配,而W的列数是不受限的,所以W的列才是特征。
另外,在此例中b应该是1*4的矩阵,意味着每个图像在考虑同一个特征时,其所加的偏置都是相同的。
有多少个特征就应该有多少个神经元(不确定)
Back Propagation
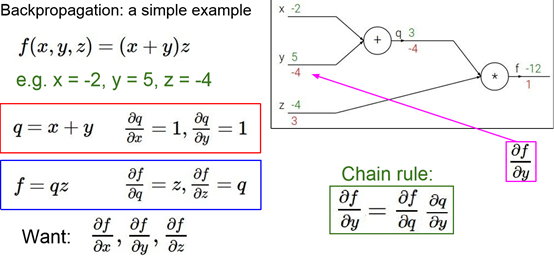
但每一项只能是很简单的结构,很重要的是要画出图!
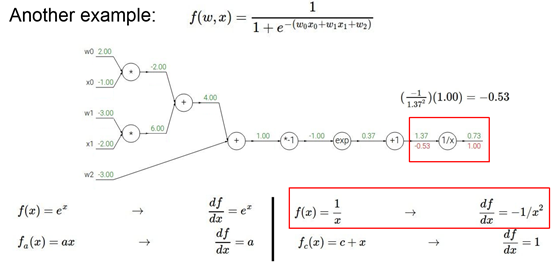
1作为local值,求1/x节点的值,则1.37作为x值,求-1/x^2
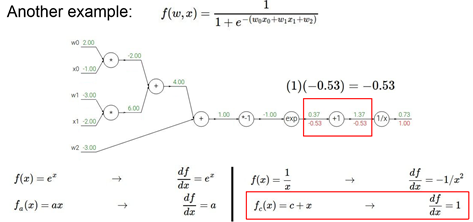
继续对+1求导为1,意味着1要乘以之前节点的值-0.53=-0.53
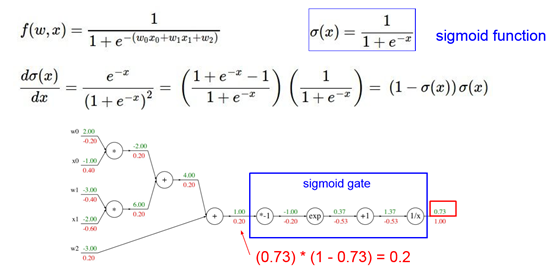
可以把一些计算整合起来作为1个node
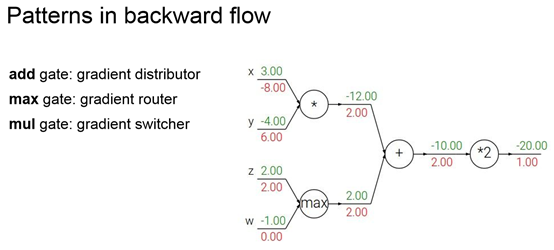
Max可以看作是选择其中一个通道进行梯度传递,而mul可以看成是交换梯度
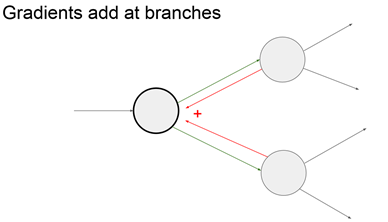
Node的梯度由branch相加
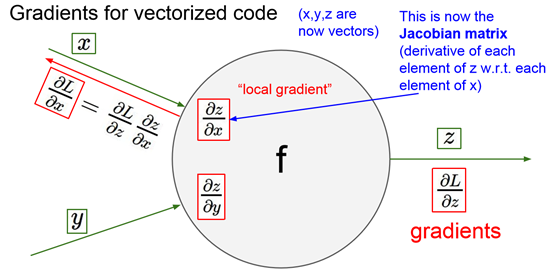
当是矩阵表示时,采用雅可比矩阵。但实际上不需要把雅可比矩阵明写,只需要知道每个x和每个y的对应关系即可。
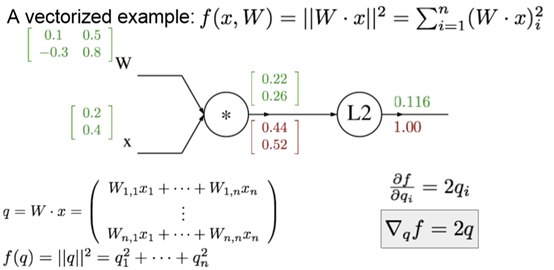
矩阵back propagation时,矩阵大小是相同的,如图红色矩阵和上面绿色矩阵是一样的,而每个元素的表达的是对应绿色矩阵的元素相对于L2的梯度。
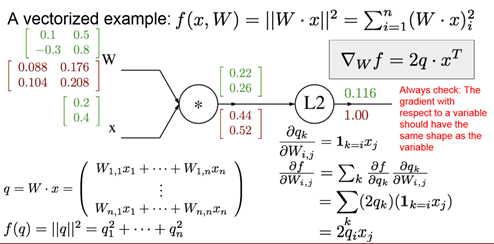
e.g. W12x2是q1的一个项,所以W12的梯度等于x2q1的梯度=0.4*0.44=0.176

可以从雅可比矩阵的角度分析:即左边红色矩阵为W的雅可比矩阵,元素1.1是中间红色矩阵第一项对W1.1的梯度。元素1.2是红色矩阵第1项对W1.2的梯度。



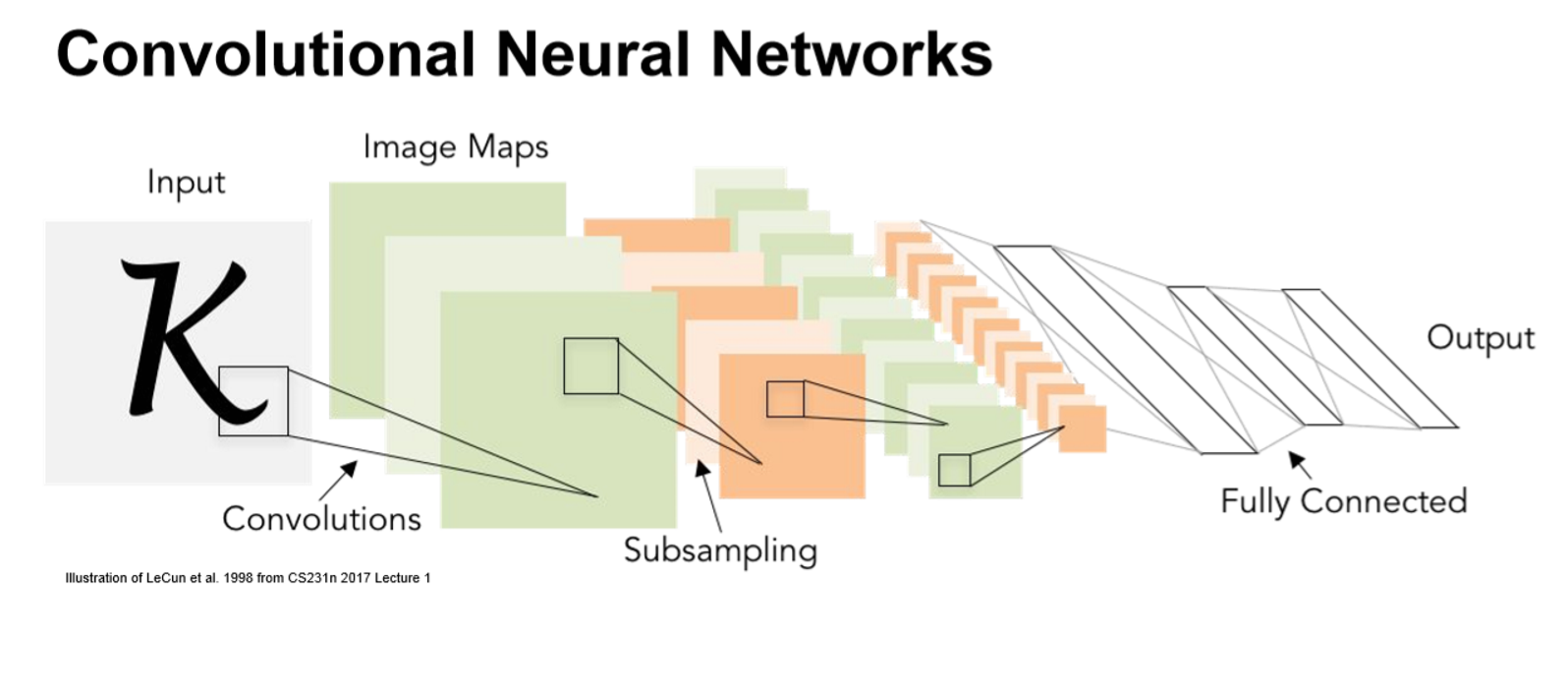
L5: Convolutional Neural Networks
Convolutions
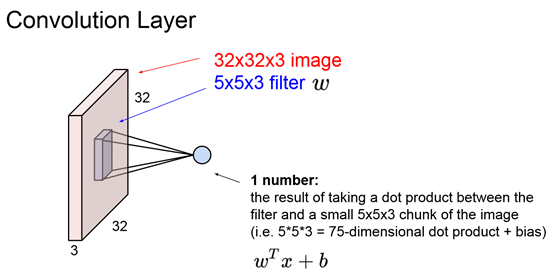
注意:CNN所说的卷积,实际上并不需要如信号与系统中,对一个轴进行反转操作。而是借用了卷积时不断平移的特性,所以称为卷积神经网络。注意相较前面处理图像时把32323展开成一维数组,CNN中是同时考虑多层的效果。而且采用的是点乘。
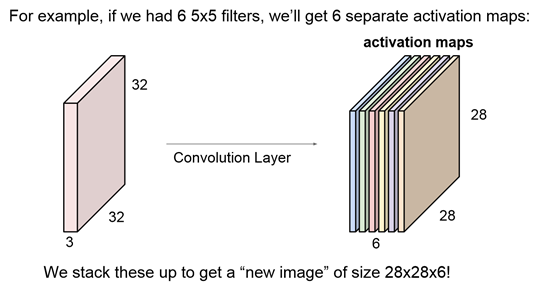
采用多个filter就能够生成多个activation maps

更像是correlation
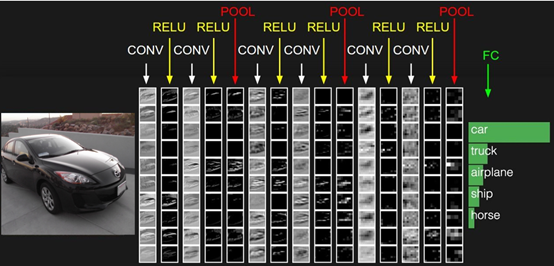
一个例子:POOL用来downsample,CNN最后会有fully connected network去计算每一类的得分。分为4部分,CONV,RELU,POOL,FC
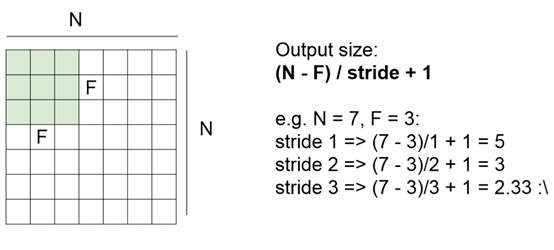
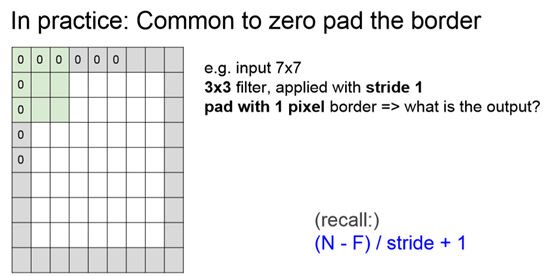
好处是左上角的数据点在填补了0后,可以作为filter的中心;可以使下一层的大小和这一层相同,避免size越来越小。而F不同,zero层数不同

不一定是填0,根据filter大小有公式可以计算zero padding的值
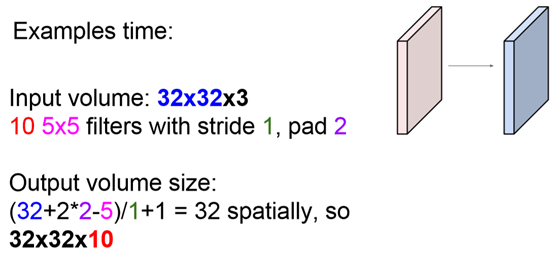
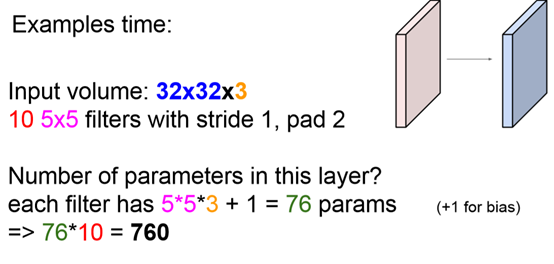
一定要记得,每个filter都是多层的,而不是二维的

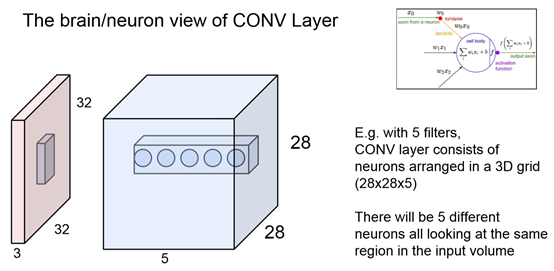
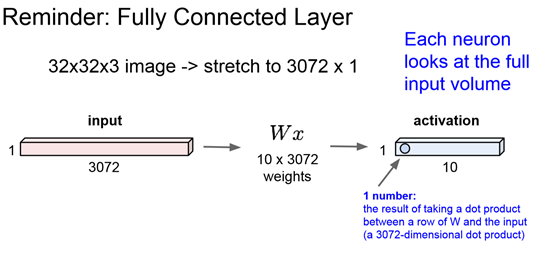
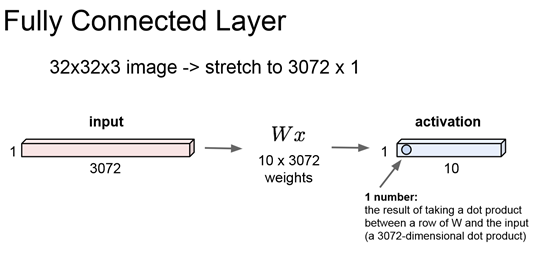
前面两张图对比CNN和之前的Fully connected layer: CNN每个元素只关注一小部分data,同时会因为有多个filter所以会有多个元素关注同一个区域。而Fully connected layer的每个元素关注的是一个input中所有的数据,因为它是W的一行×input一整列的加和值。
Pooling
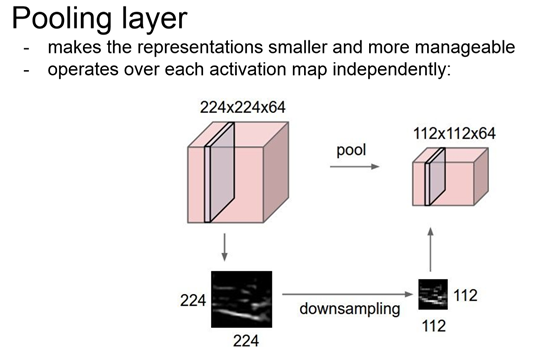
Pool的作用是downsample,用一个典型值代替这个region,一般不overlap
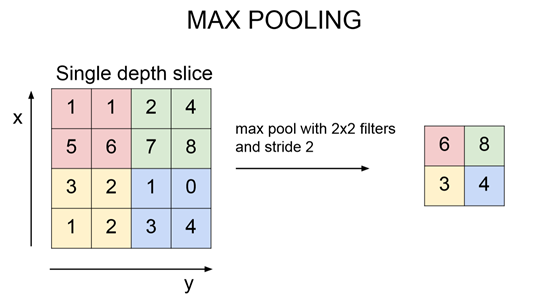
其中一种方式是Max pooling,表示:这个神经元在这个位置激发了多少能量

Activation
第一个问题:为什么引入非线性激励函数?
如果不用激励函数(其实相当于激励函数是f(x) = x),在这种情况下你每一层输出都是上层输入的线性函数,很容易验证,无论你神经网络有多少层,输出都是输入的线性组合,与没有隐藏层效果相当,这种情况就是最原始的感知机(Perceptron)了。
正因为上面的原因,我们决定引入非线性函数作为激励函数,这样深层神经网络就有意义了(不再是输入的线性组合,可以逼近任意函数)。最早的想法是sigmoid函数或者tanh函数,输出有界,很容易充当下一层输入。
第二个问题:为什么引入Relu /‘reilju/呢?
第一,采用sigmoid等函数,算激活函数时(指数运算),计算量大,反向传播求误差梯度时,求导涉及除法,计算量相对大,而采用Relu激活函数,整个过程的计算量节省很多。
第二,对于深层网络,sigmoid函数反向传播时,很容易就会出现梯度消失的情况(在sigmoid接近饱和区时,变换太缓慢,导数趋于0,这种情况会造成信息丢失。
L6: Training Neural Networks I


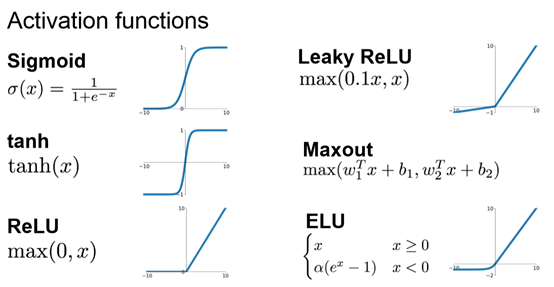
Activation function
为什么需要激励函数:因为线性函数并不能完全表示数据之间的关系,通过Activation Function(非线性函数)来把线性Y=WX给掰弯。确保可以微分,才能back propagation.
当层数只有两层的时候,任意AF都是可以尝试的,但是当层数很多时,得慎重选择AF,不然可能会出现梯度爆炸和梯度消失的现象。
CNN用Relu
RNN用Relu,tanh
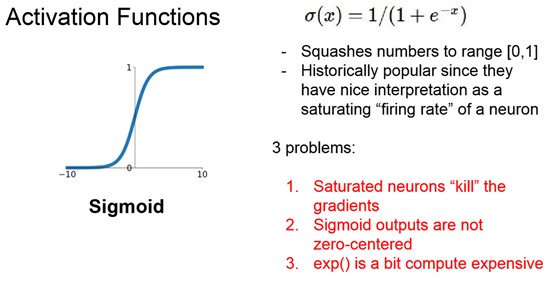

1.x取两端时,导数为0
2.local gradient是X加和,如果x是恒正的,所以local gradient是恒正的,如果上一级传下来的梯度是正/负,则该级梯度为正/负。结果就是W全部增加或W全部减小。 右图,绿色区域为梯度方向,若最优方向为第四象限,那么Sigmoid函数不能直接向着第四象限,而是需要zig zag
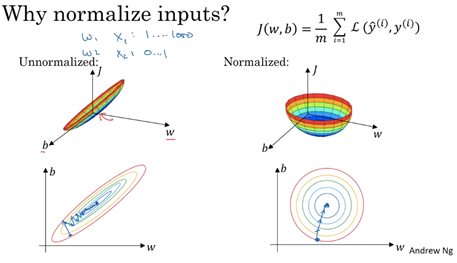
这也是为什么我们需要把data先归一化为平均值为0


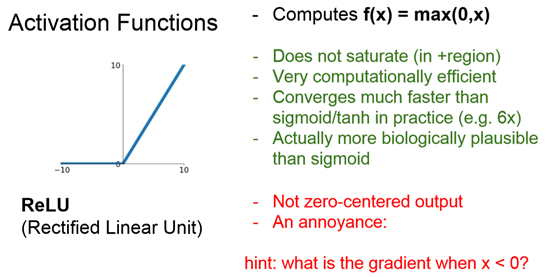
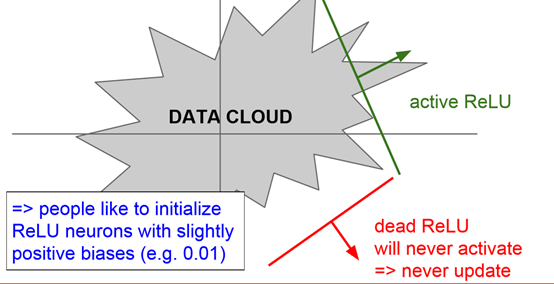
dead ReLU是无效分界线,因为位于data cloud外部,而且不会得到更新。当步长设置过大时,有可能出现dead ReLU
dead ReLU是一个超平面,一半是正,一半被kill



最后需要注意一点:在同一个网络中混合使用不同类型的神经元是非常少见的,虽然没有什么根本性问题来禁止这样做
一句话:“那么该用那种呢?”用ReLU非线性函数。注意设置好学习率,或许可以监控你的网络中死亡的神经元占的比例。如果单元死亡问题困扰你,就试试Leaky ReLU或者Maxout,不要再用sigmoid了。也可以试试tanh,但是其效果应该不如ReLU或者Maxout。
Data Preprocessing
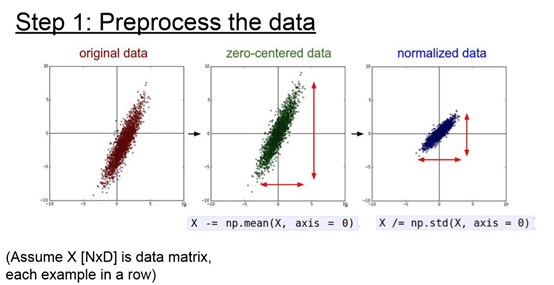
在图像处理中,不需要太多的规范化,但广泛的机器学习任务(有很多特征的…)则需要
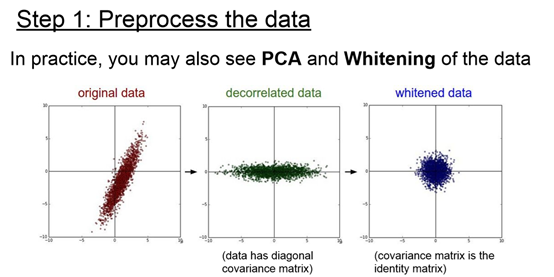
记住:在对训练集做处理的时候,也要同时对测试集做处理!
常见错误。进行预处理很重要的一点是:任何预处理策略(比如数据均值)都只能在训练集数据上进行计算,算法训练完毕后再应用到验证集或者测试集上。例如,如果先计算整个数据集图像的平均值然后每张图片都减去平均值,最后将整个数据集分成训练/验证/测试集,那么这个做法是错误的。应该怎么做呢?应该先分成训练/验证/测试集,只是从训练集中求图片平均值,然后各个集(训练/验证/测试集)中的图像再减去这个平均值。

对于CIFAR-10的处理: 减去mean image指RGB层各自减去全体RGB的mean
Weight Initialization
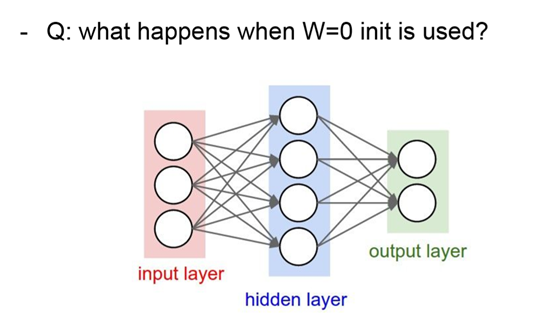
问题:如果初始矩阵都是0,那么每个神经元学习到的东西都是相同的,这和我们的愿望是违背的。
是因为如果所有的参数都是0,那么所有神经元的输出都将是相同的,那在back propagation的时候同一层内所有神经元的行为也是相同的 —- gradient相同,weight update也相同。这显然是一个不可接受的结果。

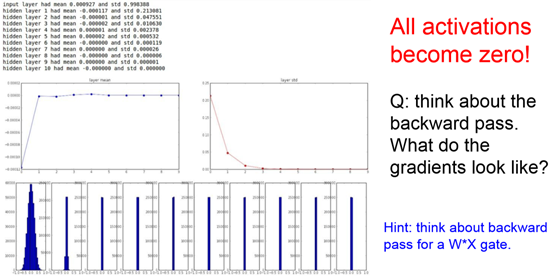
Weight很小时:XW乘积越来越趋近于1,问题是backpropagate时local gradient=0,各层几乎不变化.
小随机数初始化。因此,权重初始值要非常接近0又不能等于0。解决方法就是将权重初始化为很小的数值,以此来打破对称性。其思路是:如果神经元刚开始的时候是随机且不相等的,那么它们将计算出不同的更新,并将自身变成整个网络的不同部分。小随机数权重初始化的实现方法是:W = 0.01 * np.random.randn(D,H)。其中randn函数是基于零均值和标准差的一个高斯分布(译者注:国内教程一般习惯称均值参数为期望μ)来生成随机数的。根据这个式子,每个神经元的权重向量都被初始化为一个随机向量,而这些随机向量又服从一个多变量高斯分布,这样在输入空间中,所有的神经元的指向是随机的。也可以使用均匀分布生成的随机数,但是从实践结果来看,对于算法的结果影响极小。
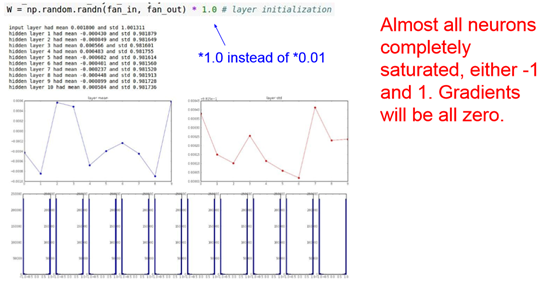
Weight大:XW会saturate,经常会在saturate region(很正或很负),all gradient=0
几乎所有的值集中在-1或1附近,神经元saturated了!注意到tanh在-1和1附近的gradient都接近0,这同样导致了gradient太小,参数难以被更新。
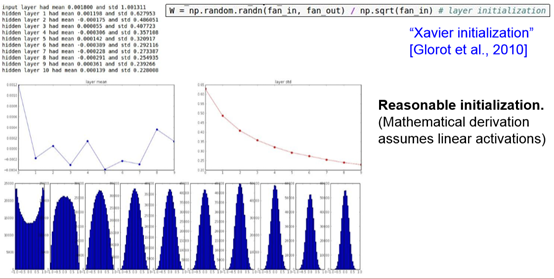
- Xavier initialization
使用1/sqrt(n)校准方差。上面做法存在一个问题,随着输入数据量的增长,随机初始化的神经元的输出数据的分布中的方差也在增大。我们可以除以输入数据量的平方根来调整其数值范围,这样神经元输出的方差就归一化到1了。也就是说,建议将神经元的权重向量初始化为:w = np.random.randn(n) / sqrt(n)。其中n是输入数据的数量。这样就保证了网络中所有神经元起始时有近似同样的输出分布。实践经验证明,这样做可以提高收敛的速度。


之前谈到Xavier initialization是在线性函数上推导得出,这说明它对非线性函数并不具有普适性,所以这个例子仅仅说明它对tanh很有效,那么对于目前最常用的ReLU神经元呢 继续做一下实验:
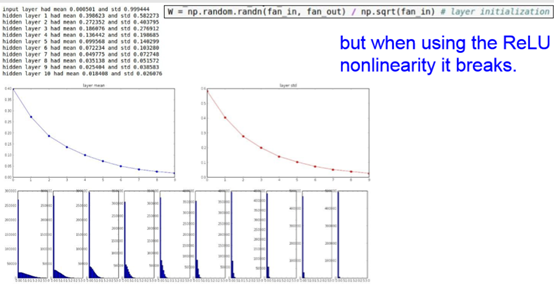
前面看起来还不错,后面的趋势却是越来越接近0。幸运的是,He initialization可以用来解决ReLU初始化的问题。
- He initialization
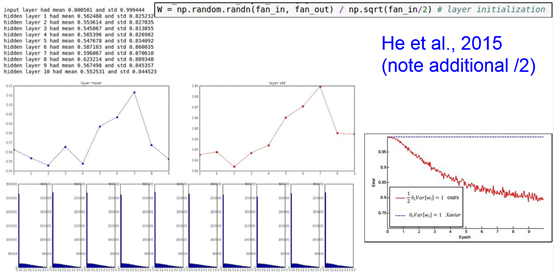
He initialization的思想是:在ReLU网络中,假定每一层有一半的神经元被激活,另一半为0,所以,要保持variance不变,只需要在Xavier的基础上再除以2:
看起来效果非常好,推荐在ReLU网络中使用!
Barch Normalization
批量归一化(Batch Normalization)。批量归一化是loffe和Szegedy最近才提出的方法,该方法减轻了如何合理初始化神经网络这个棘手问题带来的头痛:),其做法是让激活数据在训练开始前通过一个网络,网络处理数据使其服从标准高斯分布。因为归一化是一个简单可求导的操作,所以上述思路是可行的。在实现层面,应用这个技巧通常意味着全连接层(或者是卷积层,后续会讲)与激活函数之间添加一个BatchNorm层。对于这个技巧本节不会展开讲,因为上面的参考文献中已经讲得很清楚了,需要知道的是在神经网络中使用批量归一化已经变得非常常见。在实践中,使用了批量归一化的网络对于不好的初始值有更强的鲁棒性。最后一句话总结:批量归一化可以理解为在网络的每一层之前都做预处理,只是这种操作以另一种方式与网络集成在了一起。搞定!
Batch Normalization是一种巧妙而粗暴的方法来削弱bad initialization的影响,其基本思想是:If you want it, just make it!


N个数据,D个特征;是对每一个特征都做一次高斯标准化

X已经是标准化后的输出,而我们还可以引入γ和β参数,使得这个标准正态分布进行一定的移动和压缩,使得更适合下一层的使用。这些参数都是可以被训练的。
如果进行Batch normalization是对这个网络不利的,那么网络还能自己学会通过两个参数去把BN层给抵消掉!
Batch Normalization很重要的作用是:减少对初始化的依赖
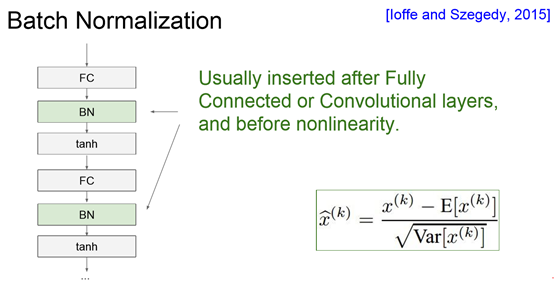
注意BN的位置!在非线性activation之前,输出值应该有比较好的分布。Batch Normalization想达到的目的是,强行把batch标准化为正态分布。
它是一种对原始数据的shift成0-mean和scale by variance,并不会影响数据的structure

需要注意的是:在用模型进行预测的时候,不再需要计算均值和方差,而是用训练时确定下来的经验均值和方差。【这和前面所说所说的预处理方法是类似的,即将全体数据集划分为训练/验证/测试,然后所有的数据集是减去训练集中的mean,而不是各自减去各自的mean】【这样做的意义在于,规范化的过程对于模型来说是一个属性,所以用该模型进行验证/测试时,都要保证这个过程是相同的,这样才能确保准确性得以维持】
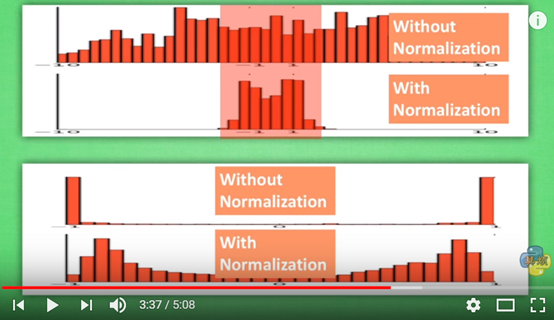
可以看到,进行过batch normalization的数据更加集中于红色的有效区域(对于tanh激活函数),经过激活函数的结果也更加的理想!
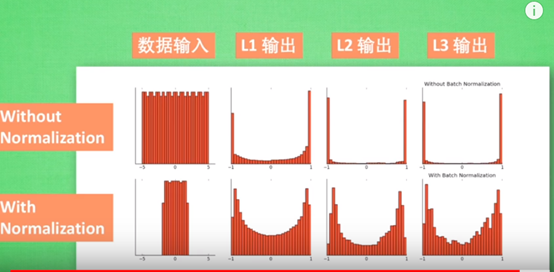
Babysitting the Learning Process
Step 1: Preprocess the data
Step 2: Choose the architecture
Step 3:Double check that the loss is reasonable
注:
一次epoch=所有训练数据forward+backward后更新参数的过程。
一次iteration=[batch size]**个**训练数据forward+backward后更新参数过程。
另:一般是iteration译成“迭代”一个epoch里面,iteration次数=batch个数(epoch/batch size)
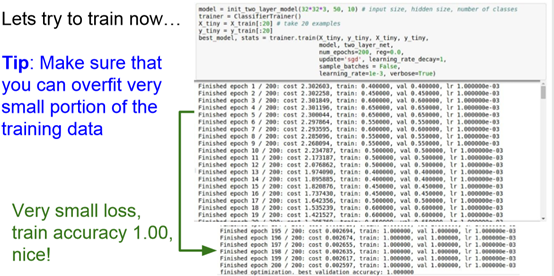
- Step 4:Start with small regularization and find learning rate that makes the loss go down


(NAN通常是损失爆炸)
Hyperparameter Optimization

一开始可以只是用少量样本,确定大致的范围。
Cross-validation是指train on your training set, and evaluate on validation set 这个超参量怎么样。
通过超参量的循环使用,可以看出每个超参量对loss的影响,进而帮助选择最优的超参量。
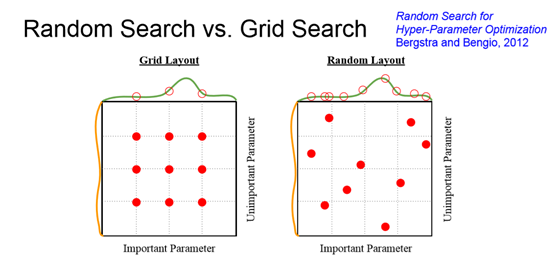
散的各个超参量取值反而有更好的效果。

我们可以处理的超参量有很多种。